Contents
Index
Stockpile Volume
Surface
Select a Surface/Boundary fom the list.
If there none there, you need to form the triangles for a surface first.
This option computes the volume of a stockpile given a Surface for a stockpile.
Boundary strings can be used around each stockpile if necessary.
The program will first form the lower surface model using the points on the boundary string of the stockpile.
It will then form the upper surface model using all the points inside the boundary string and
compute the volume of each triangular prism formed.
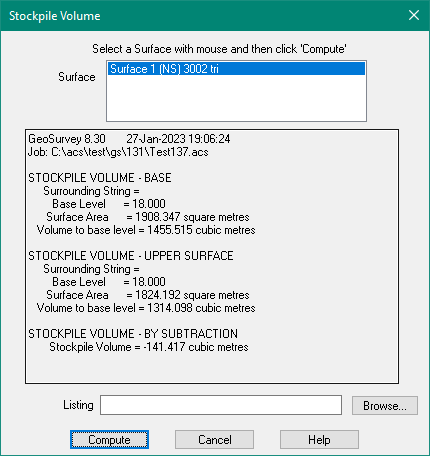
The results will be displayed on the screen and optionally written to the listing file.
Points to Note
- The base, or ‘underside’of the stockpile is assumed to be flat/planar. i.e. Prior to building the
stockpile, the natural surface is assumed to be flat/planar from one side to another. This is
important! Consider the overall size of your stockpile base and inspect 0.1m contours
within to asses the validity of the base and whether this Stockpile Volume method is
appropriate.
- Stockpile volume reports do not provide cut/fill quantities. If cut/fill is required, then a
Volume Between Surfaces should be calculated;
- The reported volume is a nett value;
- You should have a boundary string that defines the base of each stockpile;
- The stockpile can exist in amongst surrounding survey data so it does not need to be in
an isolated acs file.
Process
- Ensure stockpile bases have a single closed string.
- Inspect data, triangulate model, contour at 0.1m and resolve any errors.
- Review triangles and ensure there are no ‘holes’ (shade triangles).
- Use the menu option Topo/Stockpile Volume. Select a stockpile base string.
- Choose listing file (*.txt) – this is advisable, though not mandatory.
- Click “Compute”.
- Refer to *.txt file or copy/paste report into a file as necessary.
- Verify volume report using a common-sense approach such as calculating surface area x
average height and via an alternative method such as ‘between surfaces.’
How it Works
- User nominates stockpile surface
- GS forms triangles for bottom surface using points on the 'boundary' string
- GS computes the volume of each triangle to the base level and sums them (vol1)
- GS form triangles using all stockpile surface points
- GS computes area and volume of each triangle to the base level and sums them (vol2).
- GS computes nett stockpile volume as vol2 - vol1
- Display the results: Cut, fill volume & surface areas.
